КУТИ НА ПЛОЩИНІ ТА ЇХ ВИМІР. Фігура на площині, утворена двома променями, що виходять з однієї точки O, називається кутом. Промені OA і OB називаються сторонами кута, а точка O вершиною. Кут із сторонами OA і OB позначається Р AOB.
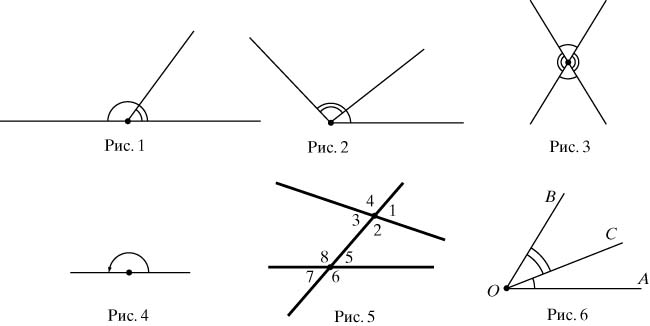
Кути порівнюють, складають, вимірюють. Вони рівні, якщо їх можна поєднати переміщенням. Два кута називаються суміжними (рис. 1), якщо у них загальні вершина і одна сторона, а дві інші утворюють пряму. Взагалі, кути, які мають спільну вершину і одну спільну сторону, називаються прилеглими (рис. 2). Кути називаються вертикальними (рис. 3), якщо сторони одного є продовженнями за вершину сторін іншого. Вертикальні кути рівні між собою. Кут, у якого сторони утворюють пряму, називається розгорнутим (рис. 4). Кут, що дорівнює своєму суміжному, називається прямим. Кут менший прямого - гострий, більший прямого, але менший розгорнутого - тупий.
При перетині двох прямих, що лежать в одній площині, третьої прямий утворюються кути (рис. 5). 1 і 5, 2 і 6, 4 і 8, 3 і 7 називаються відповідними; 2 і 5, 3 і 8 - внутрішніми односторонніми; 1 і 6, 4 і 7 - зовнішніми односторонніми; 3 і 5, 2 і 8 - внутрішніми навхрест лежать; 1 і 7, 4 і 6 - зовнішніми навхрест лежать.
Якщо промінь OC проходить всередині кута AOB (рис. 6), то, за визначенням, вважають, що кут AOC, як і кут COB, менше кута AOB і що кут AOB дорівнює сумі кутів AOC і COB. Взявши за одиницю виміру будь-якої конкретний кут, визначають величину будь-якого кута, тобто знаходять, скільки разів укладається в ньому даний одиничний кут. При вимірюванні кута виходять з двох його властивостей, аналогічних властивостям довжини відрізка: 1) величини рівних кутів рівні, 2) величина суми двох кутів дорівнює сумі їх величин.
Якщо розглянути кути, вершиною яких є центр кола, а сторонами - радіуси, то можна відзначити, що рівні кути висікають на окружності рівні дуги, і суму кутів буде відповідати сума стягуються ними дуг. Тому величина кута пропорційна довжині висікається їм дуги, і одиниці вимірювання можна задавати, вказуючи, яку частину кола становить відповідна дуга.
Зазвичай користуються двома системами вимірювання кутів: градусної і радіанної.
У градусної системі за одиницю виміру приймається дугу розміром в 1/360 окружності (позначають °). Градус ділиться на 60 хвилин (позначають '), хвилина на 60 секунд (позначають' '). Шестідесятірічних вимірювань нагадує про Вавилон, але був в історії ще один градус. За часів Великої французької революції (одна тисяча сімсот дев'яносто три) у Франції разом з десяткового (метричної) системою заходів була введена сотенна (центезімальная) система вимірювання кутів. У ній прямий кут ділиться на 100 градусів ( «градів»), градус на 100 хвилин, хвилина на 100 секунд. Ця система найбільш часто застосовується в геодезичних вимірах.
Математики вважають за краще користуватися радіанної мірою - за одиницю вимірювання приймається кут, під яким видно з центра кола її дуга, що дорівнює радіусу. Величина такого кута і є радіан. Вона не залежить від радіуса кола і від положення дуги на окружності. Оскільки півколо видно з центру під кутом 180 °, а її довжина дорівнює 241 радіусів, то радіан в 241 разів менше, ніж кут 180 °, тобто один радіан дорівнює 180 ° / 241:
1 радіан »57,2958 °» 57 ° 17'45 ''
І в радіанної і в градусної системі кут вимірюється одиницею кута. Те, що найменування в одному випадку (для градуси) проставляється, а в іншому (для радіана) мається на увазі, не має ніякого значення.
Радіанна міра, що виражається відношенням довжини дуги, описаної довільним радіусом з центру і укладеної між сторонами кута, до радіусу цієї дуги, не залежить від вибору одиниці довжини. Так само не залежить і градусна міра, тому що вона теж є відношенням двох довжин, а саме довжини дуги, описаної з вершини кута і укладеної між її сторонами, до довжини дуги рівній 1/360 частини окружності того ж радіуса.
Таким чином, ніякої принципової різниці між градусної і радіанної мірою кута немає, проте введення радіанної заходи дозволяє надати багатьом формулами більш простий вигляд.
Співвідношення градусної і радіанної заходів найбільш часто зустрічаються кутів приведено в наступній таблиці
Співвідношення градусної і радіанної заходів кутів Кути в градусах 360 ° 180 ° 90 ° 60 ° 45 ° 30 ° Кути в радіанах 2 π π π / 2 π / 3 π / 4 π / 6
Прямойугол містить в собі 90 ° або 241/2 радіан. Гострий лежить в межах від 0 до 90 ° або від 0 до 241/2 радіан, тупий - від 90 до 180 ° або від 241/2 до 241. Прямі лінії, що утворюють прямий кут, називаються перпендикулярними одна інший.
Часто важливо вказати, в якому напрямку вимірюється кут. Якщо розглядати в якості міри кута поворот навколо вершини О, переводить промінь OA в положення OB, то позитивною міра кута вважається, якщо поворот відбувається проти годинникової стрілки, в іншому випадку кут вважається негативні м. Таким чином, кут може мати своєю величиною будь-яке дійсне число. У тригонометрії таке розгляд дозволяє вивчати тригонометричні функції для будь-яких значень аргументу.
Під кутом між двома кривими, що виходять із загальної точки, в якій кожна з кривих має певну дотичну, розуміють кут, утворений цими дотичними. Поняття кута узагальнюється і на різні об'єкти в просторі (двогранні, тілесні і багатогранні кути.