- Механіка твердого тіла. Лекції. I. Обертання твердого тіла навколо нерухомої осі.
- Кінетична енергія тіла, що обертається і робота зовнішніх сил (вісь обертання нерухома).
- Вільні осі. Стійкість вільного обертання.
Механіка твердого тіла. Лекції. I. Обертання твердого тіла навколо нерухомої осі.
У цьому випадку рух твердого тіла визначається рівнянням
тут 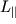 - це момент імпульсу відносно осі обертання, тобто проекція на вісь моменту імпульсу, визначеного щодо деякої точки, що належить осі ( см. лекцію 2 ).
- це момент імпульсу відносно осі обертання, тобто проекція на вісь моменту імпульсу, визначеного щодо деякої точки, що належить осі ( см. лекцію 2 ). 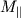 - це момент зовнішніх сил щодо осі обертання, тобто проекція на вісь результуючого моменту зовнішніх сил, певного щодо деякої точки, що належить осі, причому вибір цієї точки на осі, як і у випадку з
- це момент зовнішніх сил щодо осі обертання, тобто проекція на вісь результуючого моменту зовнішніх сил, певного щодо деякої точки, що належить осі, причому вибір цієї точки на осі, як і у випадку з 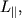 значення не має. Дійсно (рис. 3.4),
значення не має. Дійсно (рис. 3.4), 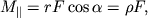 де
де 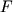 - складова сили, прикладеної до твердого тіла, перпендикулярна осі обертання,
- складова сили, прикладеної до твердого тіла, перпендикулярна осі обертання, 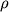 - плече сили
- плече сили 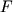 щодо осі.
щодо осі.
оскільки 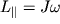 (
( 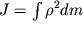 - момент інерції тіла відносно осі обертання), то замість
- момент інерції тіла відносно осі обертання), то замість  можна записати
можна записати
або
оскільки в разі твердого тіла 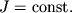
Рівняння (3.9) і є основне рівняння динаміки обертального руху твердого тіла навколо нерухомої осі . Його векторна. форма має вигляд:
вектор 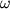 завжди спрямований уздовж осі обертання, а
завжди спрямований уздовж осі обертання, а 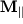 - це складова вектора моменту сили вздовж осі.
- це складова вектора моменту сили вздовж осі.
В разі 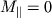 отримуємо
отримуємо 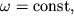 відповідно і момент імпульсу відносно осі
відповідно і момент імпульсу відносно осі 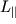 зберігається. При цьому сам вектор L, визначений щодо будь-якої точки на осі обертання, може змінюватися. Приклад такого руху показаний на рис. 3.5.
зберігається. При цьому сам вектор L, визначений щодо будь-якої точки на осі обертання, може змінюватися. Приклад такого руху показаний на рис. 3.5.
Стрижень АВ, шарнірно закріплений в точці А, обертається за інерцією навколо вертикальної осі таким чином, що кут 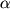 між віссю і стрижнем залишається постійним. Вектор моменту імпульсу L, щодо точки А рухається по конічний поверхні з кутом полураствора
між віссю і стрижнем залишається постійним. Вектор моменту імпульсу L, щодо точки А рухається по конічний поверхні з кутом полураствора 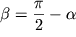 проте проекція L на вертикальну вісь залишається постійною, оскільки момент сили тяжіння відносно цієї осі дорівнює нулю.
проте проекція L на вертикальну вісь залишається постійною, оскільки момент сили тяжіння відносно цієї осі дорівнює нулю.
Кінетична енергія тіла, що обертається і робота зовнішніх сил (вісь обертання нерухома).
Швидкість i -й частки тіла
де 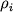 - відстань частинки до осі обертання Кінетична енергія
- відстань частинки до осі обертання Кінетична енергія
так як кутова швидкість обертання для всіх точок однакова.
Відповідно до законом зміни механічної енергії системи елементарна робота всіх зовнішніх сил дорівнює приросту кінетичної енергії тіла:
Робота зовнішніх сил при повороті тіла на кінцевий кут 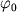 дорівнює
дорівнює
опустимо, що диск точила обертається по інерції з кутове швидкістю 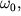 і ми зупиняємо його, притискаючи який-небудь предмет до краю диска з постійним зусиллям. При цьому на диск буде діяти постійна за величиною сила
і ми зупиняємо його, притискаючи який-небудь предмет до краю диска з постійним зусиллям. При цьому на диск буде діяти постійна за величиною сила 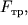 спрямована перпендикулярно його осі. Робота цієї сили
спрямована перпендикулярно його осі. Робота цієї сили
де  - радіус диска,
- радіус диска, 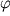 - кут його повороту. Число обертів , Яке зробить диск до повної зупинки,
- кут його повороту. Число обертів , Яке зробить диск до повної зупинки,
де 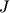 - момент інерції диска точила разом з якорем електромотора.
- момент інерції диска точила разом з якорем електромотора.
Зауваження. Якщо сили такі, що 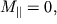 то роботу вони не виробляють.
то роботу вони не виробляють.
Вільні осі. Стійкість вільного обертання.
При обертанні тіла навколо нерухомої осі ця вісь утримується в незмінному положенні підшипниками. При обертанні незбалансованих частин механізмів осі (вали) відчувають певну динамічну навантаження, Виникають вібрації, тряска, і механізми можуть зруйнуватися.
Якщо тверде тіло розкрутити навколо довільної осі, жорстко пов'язаної з тілом, і вивільнити вісь з підшипників, то її напрямок в просторі, взагалі кажучи, буде змінюватися. Для того, щоб довільна вісь обертання тіла зберігала свій напрямок незмінним, до неї необхідно докласти певних сили. Виникаючі при цьому ситуації показані на рис. 3.6.
Як обертового тіла тут використаний масивний однорідний стрижень АВ, прикріплений до досить еластичною осі (зображена подвійними штриховими лініями). Еластичність осі дозволяє візуалізувати відчувають нею динамічні навантаження. У всіх випадках вісь обертання вертикальна, жорстко пов'язана зі стрижнем і укріплена в підшипниках; стрижень розкручений навколо цієї осі і наданий сам собі.
У разі, зображеному на рис. 3.6а, вісь обертання є для точки В стержня головною, але не центральною, 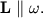 Ось згинається, з боку осі на стрижень діє сила
Ось згинається, з боку осі на стрижень діє сила 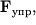 забезпечує його обертання (в НІСО, пов'язаної зі стрижнем, ця сила врівноважує відцентрову силу інерції). З боку стрижня на вісь діє сила
забезпечує його обертання (в НІСО, пов'язаної зі стрижнем, ця сила врівноважує відцентрову силу інерції). З боку стрижня на вісь діє сила 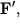 врівноважена силами
врівноважена силами  з боку підшипників.
з боку підшипників.
У разі рис. 3.6б вісь обертання проходить через центр мас стержня і є для нього центральної, але не головною. Момент імпульсу відносно центру мас О не зберігається і описує конічну поверхню. Ось складним чином деформується (ізламивается), з боку осі на стрижень діють сили 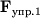 і
і 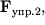 момент яких забезпечує приріст
момент яких забезпечує приріст 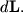 (В НІСО, пов'язаної зі стрижнем, момент пружних сил компенсує момент відцентрових сил інерції, що діють на одну і іншу половини стрижня). З боку стрижня на вісь діють сили
(В НІСО, пов'язаної зі стрижнем, момент пружних сил компенсує момент відцентрових сил інерції, що діють на одну і іншу половини стрижня). З боку стрижня на вісь діють сили 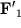 і
і 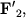 спрямовані протилежно силам
спрямовані протилежно силам 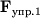 і
і 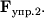 момент сил
момент сил 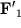 і
і 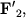 урівноважений моментом сил
урівноважений моментом сил 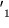 і
і 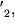 що виникають в підшипниках.
що виникають в підшипниках.
І тільки в тому випадку, коли вісь обертання збігається з головною центральною віссю інерції тіла (ріс.3.6в), розкручений і наданий сам собі стрижень не робить на підшипники ніякого впливу. Такі осі називають вільними осями, тому що, якщо прибрати підшипники, вони будуть зберігати свій напрямок в просторі незмінним.
Інша річ, чи буде це обертання стійким по відношенню до малих збурень, завжди мають місце в реальних умовах. Досліди показують, що обертання навколо головних центральних осей з найбільшим і найменшим моментами інерції є стійким, а обертання навколо осі з проміжним значенням моменту інерції - нестійким. У цьому можна переконатися, підкидаючи вгору тіло у вигляді паралелепіпеда, розкручене навколо однієї з трьох взаємно перпендикулярних головних центральних осей (рис. 3.7). Ось AA 'відповідає найбільшому, вісь BB' - середнього, а вісь CC '- найменшому моменту інерції паралелепіпеда. Якщо підкинути таке тіло, повідомивши йому швидке обертання навколо осі AA 'або навколо осі CC', можна переконатися в тому, що це обертання є цілком стійким. Спроби змусити тіло обертатися навколо осі BB 'до успіху не приводять - тіло рухається складним чином, перекидаючись в польоті.
У тілах обертання стійкої виявляється вільна вісь, відповідна найбільшому моменту інерції. Так, якщо суцільний однорідний диск підвісити до бистровращающейся валу електромотора (рис. 3.8, вісь обертання вертикальна), то диск досить швидко займе горизонтальне положення, стійко обертаючись навколо центральної осі, перпендикулярної до площини диска.
назад | вперед
Подивитися коментарі
[3]
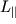 - це момент імпульсу відносно осі обертання, тобто проекція на вісь моменту імпульсу, визначеного щодо деякої точки, що належить осі ( см. лекцію 2 ).
- це момент імпульсу відносно осі обертання, тобто проекція на вісь моменту імпульсу, визначеного щодо деякої точки, що належить осі ( см. лекцію 2 ). 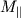 - це момент зовнішніх сил щодо осі обертання, тобто проекція на вісь результуючого моменту зовнішніх сил, певного щодо деякої точки, що належить осі, причому вибір цієї точки на осі, як і у випадку з
- це момент зовнішніх сил щодо осі обертання, тобто проекція на вісь результуючого моменту зовнішніх сил, певного щодо деякої точки, що належить осі, причому вибір цієї точки на осі, як і у випадку з 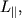 значення не має. Дійсно (рис. 3.4),
значення не має. Дійсно (рис. 3.4), 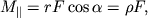 де
де 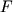 - складова сили, прикладеної до твердого тіла, перпендикулярна осі обертання,
- складова сили, прикладеної до твердого тіла, перпендикулярна осі обертання, 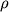 - плече сили
- плече сили 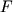 щодо осі.
щодо осі. 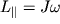 (
( 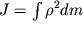 - момент інерції тіла відносно осі обертання), то замість
- момент інерції тіла відносно осі обертання), то замість  можна записати
можна записати 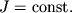
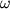 завжди спрямований уздовж осі обертання, а
завжди спрямований уздовж осі обертання, а 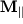 - це складова вектора моменту сили вздовж осі.
- це складова вектора моменту сили вздовж осі. 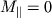 отримуємо
отримуємо 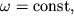 відповідно і момент імпульсу відносно осі
відповідно і момент імпульсу відносно осі 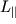 зберігається. При цьому сам вектор L, визначений щодо будь-якої точки на осі обертання, може змінюватися. Приклад такого руху показаний на рис. 3.5.
зберігається. При цьому сам вектор L, визначений щодо будь-якої точки на осі обертання, може змінюватися. Приклад такого руху показаний на рис. 3.5. 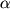 між віссю і стрижнем залишається постійним. Вектор моменту імпульсу L, щодо точки А рухається по конічний поверхні з кутом полураствора
між віссю і стрижнем залишається постійним. Вектор моменту імпульсу L, щодо точки А рухається по конічний поверхні з кутом полураствора 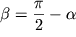 проте проекція L на вертикальну вісь залишається постійною, оскільки момент сили тяжіння відносно цієї осі дорівнює нулю.
проте проекція L на вертикальну вісь залишається постійною, оскільки момент сили тяжіння відносно цієї осі дорівнює нулю. 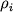 - відстань частинки до осі обертання Кінетична енергія
- відстань частинки до осі обертання Кінетична енергія 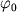 дорівнює
дорівнює 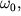 і ми зупиняємо його, притискаючи який-небудь предмет до краю диска з постійним зусиллям. При цьому на диск буде діяти постійна за величиною сила
і ми зупиняємо його, притискаючи який-небудь предмет до краю диска з постійним зусиллям. При цьому на диск буде діяти постійна за величиною сила 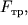 спрямована перпендикулярно його осі. Робота цієї сили
спрямована перпендикулярно його осі. Робота цієї сили  - радіус диска,
- радіус диска, 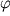 - кут його повороту. Число обертів , Яке зробить диск до повної зупинки,
- кут його повороту. Число обертів , Яке зробить диск до повної зупинки, 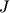 - момент інерції диска точила разом з якорем електромотора.
- момент інерції диска точила разом з якорем електромотора. 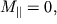 то роботу вони не виробляють.
то роботу вони не виробляють. 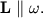 Ось згинається, з боку осі на стрижень діє сила
Ось згинається, з боку осі на стрижень діє сила 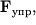 забезпечує його обертання (в НІСО, пов'язаної зі стрижнем, ця сила врівноважує відцентрову силу інерції). З боку стрижня на вісь діє сила
забезпечує його обертання (в НІСО, пов'язаної зі стрижнем, ця сила врівноважує відцентрову силу інерції). З боку стрижня на вісь діє сила 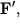 врівноважена силами
врівноважена силами  з боку підшипників.
з боку підшипників. 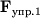 і
і 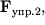 момент яких забезпечує приріст
момент яких забезпечує приріст 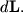 (В НІСО, пов'язаної зі стрижнем, момент пружних сил компенсує момент відцентрових сил інерції, що діють на одну і іншу половини стрижня). З боку стрижня на вісь діють сили
(В НІСО, пов'язаної зі стрижнем, момент пружних сил компенсує момент відцентрових сил інерції, що діють на одну і іншу половини стрижня). З боку стрижня на вісь діють сили 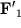 і
і 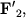 спрямовані протилежно силам
спрямовані протилежно силам 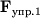 і
і 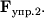 момент сил
момент сил 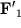 і
і 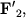 урівноважений моментом сил
урівноважений моментом сил 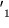 і
і 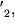 що виникають в підшипниках.
що виникають в підшипниках. Подивитися коментарі









